Margin Probabilities from NFL Spreads

Looking to calculate the cover probability of a pre-game spread? Try the nfelo cover probability calculator

Summary

• NFL final margins follow a somewhat normal distribution around the spread, but modeling the probability of specific margin outcomes is made difficult by the higher frequency of key numbers

• Representing key numbers as their own distributions to be combined into a single mixed probability model yields more accurate predictions that can be generalized for any spread

• A generalized model for margin probabilities given a spread can power a better framework for assessing the expected value of a bet, which, in turn, can lead to smarter wagering strategies

Margin Distributions in the NFL

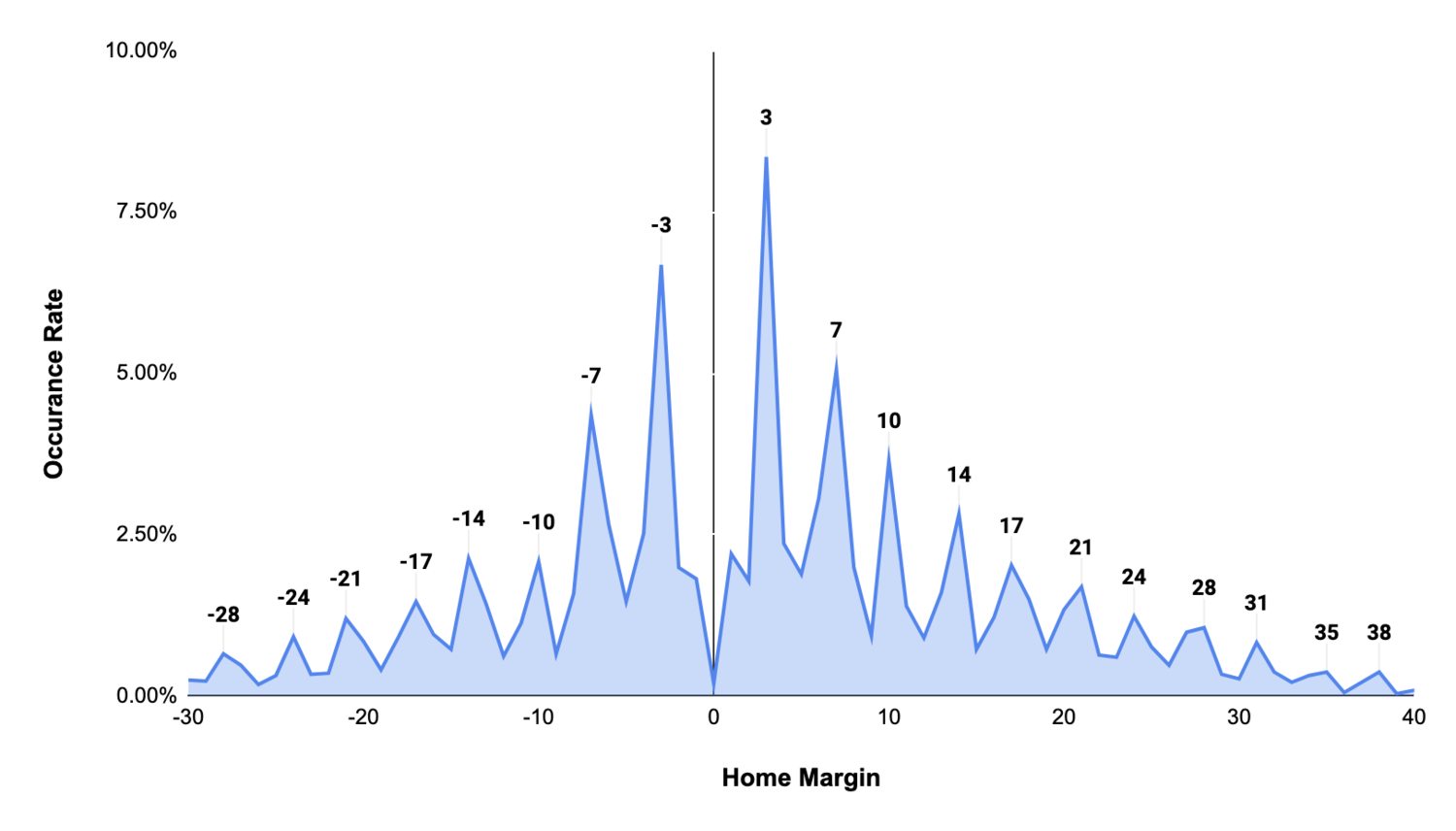
NFL spreads are a remarkable predictor of not just winners and losers, but also final margins. Over a large enough sample, roughly 50% of final margins will fall above the spread and 50% below. Spreads also provide guidance on the margin of victory itself. Margins closer to the spread are more likely to occur than those further away.

With the average home team expected to win by ~2 points (the Home Field Advantage), it’s unsurprising that home margins follow a normal(ish) distribution around this number:

From a modeling standpoint, a general normal distribution yields a simple, but directionally accurate estimate of a home team’s probability to win or lose by “X” points:

There are, however, clear shortcomings in this approach. Scoring increments in football (7, 3, 2, etc), cause certain margins to occur more frequently than others. These are referred to as “key numbers:”

To better model expected margin, each key number can be thought of as its own normal distribution, weighted by a baseline normal distribution around the original spread. Said another way, all key numbers have the same individual distributions, but the weight of those distributions towards the aggregate distribution decreases as the key number in question moves further away from the predicted spread:

Though this approach provides a better representation of actual margin likelihoods, it can be improved. Weighting key number distributions with a more complex underlying distribution, like the super gaussians show below, yields increased control and a better fit:

Combining the original baseline normal distribution and super gaussian weighted key number distributions creates a significantly more accurate representation of margin likelihoods:

Because NFL game outcomes are binary (i.e. one team wins and one team loses), a normal distribution does appear to underfit the probability of loss outcomes. Even though -3 and -7 are roughly equal in distance from the mean (2.1) as 7 and 10, they occur with higher frequency.

To account for the binary nature of games, a final multiplier can be added to outcomes on the “other” side of the spread--overweighting negative outcomes when the spread is positive, and positive ones when the spread is negative. To avoid overestimating long tail losses, this multiplier can, itself, be discounted by another normal distribution centered at the mean. Combining all of these factors together creates an even more accurate representation of final margins:

A more subjective decision can (and will) be made to force 50% of the distribution to fall on either side of the predicted spread. It’s critical to note that the model is meant to predict final margins based on a modeled win probability, not a market spread. Predicted margins should always fall evenly on either side of our win probability estimate, even if this requirement may not necessarily be observed in the underlying training dataset, which is based on imperfect market signals and small sample sizes.

Generalization

On average, home teams win by 2.1 points, but a home team favored by more or less than that number has a different expected margin of victory. The model described above allows for generalization by changing the centerpoint (i.e. mean) of the baseline and weighting distributions. For instance, changing the mean of all weighting distributions to 10 shifts the centerpoint of the overall distribution to the right and changes the weighting of key numbers to reflect their proximity to that new number:

The key advantage of this approach is its preservation of the normal distribution around the spread. The likelihood of all margins above or below the spread remains 50%, while the likelihood of individual margins are increased and decreased.

The second advantage of this approach is its ability to fit to any spread. Not every spread has occurred frequently enough to observe an even distribution of margins. Using only observed margins for spreads of 10 to model future spreads of 10 will result in lumpy  predictions, as the observed distributions themselves are fairly uneven:

Shifting the model out to be centered around 10--without changing any of the model’s underlying distribution parameters--yields a fit that passes the eye test:

Model Fitting

With the goal of the model being a generalization of margins given a spread, the ideal parameters for the model and its underlying distributions are those that minimize the error between predicted and observed occurrence rates of different margins.

The model parameters are defined as:

With the modeled probability for a home margin result given a home spread defined as:

To structure the optimization, a table of all possible combinations of spreads and point differentials between -75 and 75 was created. For each combination, a modeled probability was created and then normalized so that all probabilities for a given starting spread line summed to 1 and an equal amount of probability fell on each side of the spread.

The error for the minimization function was defined as the RMSE between modeled likelihoods and observed likelihoods for margins given a spread. Extreme spreads and unlikely outcomes were removed as they introduced significant noise to a dataset that calculates error across all possible spread<>margin combinations:

The multiple distribution model explains margins meaningfully better than a single normal distribution, and does not appear to suffer from any overfitting:

Application in Sports Betting

The difference between a bettor’s expectation of outcome and the market’s defines value. If a bettor believes the true line of a game should be 3.5, while the market prices it at 3, the bettor will see value in placing a bet to cover 3 (vig notwithstanding).

However, because final margins land on key numbers with greater frequency, value on a given bet can not be linearly extrapolated from the simple difference between perceived price and market price. The 0.5 point difference between 4.0 and 4.5 is not worth the same amount as the 0.5 point difference between 3.0 and 3.5. The only way to model true expected value is to model the likelihood of all possible outcomes.

A generalized model for final margins enables this analysis. Given an expected “true” line, a generalized model can predict the likelihood that the final margin lands below, on, or above, a market line:

Assuming a standard 110 price, any expected<>market line combination can be translated into an expected value for the bet:

Closing

Effective modeling of NFL margins requires a confrontation of key numbers. The probabilistic nature of football makes this quite challenging. Leveraging multiple distributions in a generalized model for key numbers provides a better estimate than a simple normal distribution and can make expected value estimates more accurate.

As a helpful reference for those not using code to create line estimates, this table provides a direct lookup of probabilities for all spread // outcome pairs. 

As always, feel free to reach out to @greerNFL on twitter for any questions or feedback on this approach!